| Objectives |
1 | Solving Right Triangles
Objective: To use trigonometry to find unknown sides or angles of a right triangle.
|
2 | The Area of a Triangle
Objective: To find the area of a triangle given the length of two sides and the measure of the included angle.
|
3 | The Law of Sines
Objective: To use the Law of Sines to find unknown parts of triangles.
|
4 | The Law of Cosines
Objective: To use the law of cosines to find unknown parts of a triangle.
|
5 | Applications of Trigonometry to Navigation and Surveying
Objective:To use trigonometry to solve navigation and surveying problems.
|
| Essential Questions |
| How can you determine if a triangle had no solution, one solution, or two solutions?
How can you solve triangles using these laws? |
| Why canít physical models of vector quantities be represented by scalar quantities? |
| Key Concepts |
Concept:1. | Solving a triangle |
Concept:2. | Area of a triangle |
Concept:3. | A segment of a circle |
Concept:4. | The Law of Sines |
Concept:5. | The Law of Cosines |
Concept:6. | Course, compass bearing |
| Content Covered |
Text Books
|
|
Online Resouces |
|
Summary and Reminders |
Reminders
- Make sure that you read the textbook before answering the questions.
Be sure that you understand the solutions to the textbook problems. There are only a
few problems per section, so if you have any questions about any of the problems you
need to ask the questions in class.
|
| Student Handouts/Resources |
|
| Trigonometry Skill Quizzes will access spcicific skills. |
| Quiz# |
Skill/Objective |
Sample Questions |
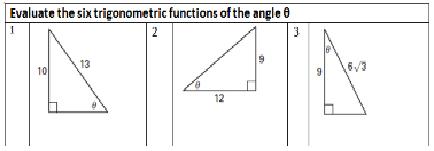
| 1 |
Evaluate the six trigonometry functions of acute angles of a right triangle. Apply the Pythagorean theorem to find missing side lengths of right triangles.
|
 |
| 2 |
Use the six trigonometry functions to solve a right triangle. To solve a triangle means to find all of the side lengths and the measure of all of the angles.
|
 |
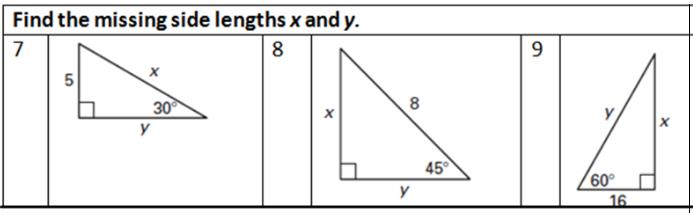
| 3 |
Use the properties of the special 30-60-90 and 45-45-90 triangles to find the missing side lengths.
|
 |
| 4 |
Use the law of sine to solve any triangle (not just right triangles).
|
 |
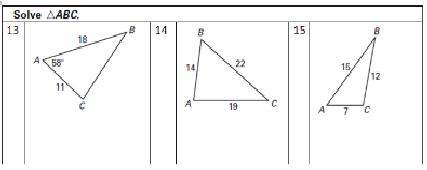
| 5 |
Use the law of cosines (and some algebra) to find the sides and angles of any triangle.
|
 |
| 6 |
Given the 3 side lengths of a triangle, determine whether the triangle is acute, obtuse, right, or whether no triangle is possible.
|
 |
| 7 |
Find the area of any triangle, when you have the measures of some sides or angles, but not the height.
For example, if you have the measure of two side lengths and the measure of the angle opposite the third side.
|
 |
| 8 |
Apply the trigonometric functions to solve problems from the real world.
|
 |
|
| 






